Het Vedisch vierkant 

Het oorspronkelijke Vedisch vierkant is een getallen vierkant van 9 x 9 vakjes. Het vierkant wordt gecreëerd volgens een methode uit de Vedische wiskunde die bij ons beter bekend is als de methode om de deelbaarheid door negen te testen. Deze methode wordt in de westers wereld ook gebruikt in de Negenproef om het resultaat van berekeningen te controleren.
De methode gaat als volgt:

Maak een vierkant van 9 x 9 vakjes waarin de tafeltjes van 1 t/m 9 geplaatst zijn. 

Vervolgens worden van de getallen die uit 2 cijfers bestaan, die 2 cijfers bij elkaar opgeteld. 81 wordt dan 8 + 1 = 9. Herhaal dit proces als er door de optelling weer een getal van 2 cijfers ontstaat. 56 wordt 5 + 6 = 11,   11 wordt 1 + 1 = 2. Indien alle getallen op deze manier bewerkt zijn ontstaat onderstaande Vedisch vierkant.

Het bovenstaande vierkant wordt in India op de zelfde manier gebruikt als bij ons het Enneagram. Er zijn zelfs sterke overeenkomsten tussen de structuur van het Enneagram en het Vedisch vierkant. Het Enneagram heeft een gespiegelde structuur die er voor zorgt dat de getallen links van de figuur gekoppeld zijn aan de getallen rechts van de figuur.
1 is gekoppeld aan 8, 2 is gekoppeld aan 7 en 4 is gekoppeld aan 5. Deze koppeling zie je ook terug bij het Vedisch vierkant als je de vakjes met gekoppelde getallen een kleur geeft zoals hieronder te zien is.  

De 9 wijkt enigszins af van de rest omdat de buitenrand van de figuur ook als deel van het Vedisch vierkant wordt gezien. De buitenrand is rekenkundig gezien ook niet correct. Het rekenkundig principe dat hier gebruikt wordt is het rekenen met modulo 9. In modulo 9 is de grootse waarde 8 en de kleinste waarde 0. Onderstaande figuur laat de in mijn ogen lelijke afwijking zien.  Indien je de 9 weglaat krijg je volmaakt symmetrische figuren.  

De relaties tussen de getallen in het Vedisch vierkant zijn zeer mooi weer te geven met behulp van de optie oppervlaktegrafieken in het programma Excel. Onderstaande figuur laat zien hoe het Vedisch vierkant er uitziet met een oppervlaktegrafiek waarbij de negens aan de randen zijn verwijderd.

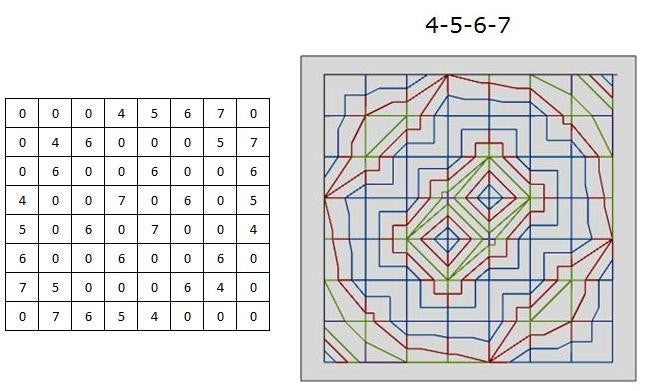
Door met selecties van getallen te werken kun je op deze manier een idee krijgen van de relaties die bestaan tussen verschillende getallen. Het aantal mogelijkheden is te groot om hier allemaal weer te geven, zodat ik hier een kleine selectie van combinaties met alleen 4 getallen laat zien.

Met behulp van het programma Excel is het mogelijk om Vedische vierkanten te maken in ieder gewenst formaat. Om dit te realiseren maken we gebruik van de modulo functie die in Excel REST wordt genoemd. Als voorbeeld ga ik uit van een vierkant dat gemaakt wordt met modulo 17. De zijden van het vierkant lopen dan van 1 t/m 16. In het onderstaande plaatje zie je dit vierkant met daarbij de formule die gebruikt moet worden voor de berekening. Ieder formaat vierkant is op deze manier met Excel te creëren. De lengte van de zijden is altijd modulo-1.

Onderstaande plaatje geeft de oppervlaktegrafiek weer van dit vierkant.

Onderstaande is een Vedisch vierkant weergegeven van 29 x 30 vakjes. De basis van dit vierkant wordt gevormd door de driehoeksgetallen en vierhoeksgetallen die zijn bewerkt met modulo 31. De getallen in het vierkant worden berekend door de horizontale en verticale getallen met elkaar te vermenigvuldigen en de uitkomst te bewerken met modulo 13. Zoals in de animatie te zien is ontstaat er voor ieder getal dat ontstaat een symmetrisch patroon. Het laatste patroon in de animatie is een samengeteld patroon dat met behulp van de oppervlakte grafiek functie van Excel is gecreëerd.  

 Onderstaande nog een voorbeeld van een Vedisch vierkant dat gegenereerd is met gebruikmaking van veelhoeksgetallen. Voor meer informatie zie mijn andere website