Het Enneagram

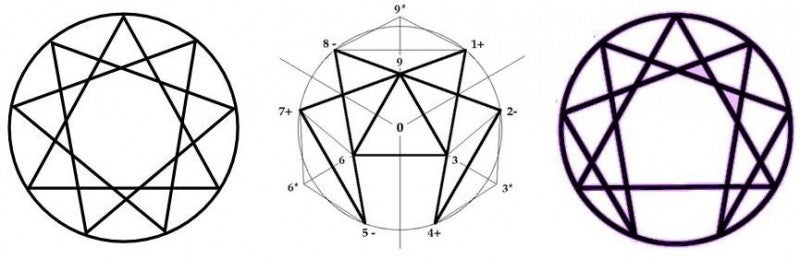
Ondanks het feit dat ik mij niet inlaat met de speculatieve wereld van het Enneagram, is dit symbool voor mij een van de krachtigste symbolen die ik ken. De mathematische  kant van dit symbool is voor mij de aanzet geweest voor een groot aantal experimenten die ik uitgevoerd heb met getallenreeksen. De resultaten van deze experimenten zijn te vinden op mijn andere website http://fiboart.jouwweb.nl. De kracht van het Enneagram ligt voor mij in de weerspiegeling van een aantal belangrijke eigenschappen van de natuur en wel symmetrie, herhaling, cyclisch gedrag en relativiteit. De gebruikers van het Enneagram in het alternatieve circuit leggen graag de nadruk op het kenmerk “oneindige beweging”. Dit kenmerk heeft ten eerste niets met de natuur te maken, omdat alles in de natuur tijdelijk van aard is, en ten tweede is het kenmerk “oneindige beweging” relatief zoals ik in het onderstaande artikel duidelijk zal maken. Het begrip oneindig heeft voor mij wel werkelijkheidswaarde met betrekking tot het bestaan, maar dit heeft niets met beweging als zodanig te maken.

Historie van het Enneagram

Het Enneagram is voor de gebruikers ervan meer dan zomaar een symbool. Het Enneagram is een systeem dat gebruikt wordt voor persoonlijkheidsanalyse vergelijkbaar met astrologie en numerologie. De beoefenaars van deze pseudowetenschap willen graag doen geloven dat dit systeem al meer dan duizend jaar oud is. Na bestudering van de feiten, ben ik tot de conclusie gekomen dat het systeem niet ouder kan zijn dan 400 jaar. Zeer waarschijnlijk is de versie zoals die op dit moment gebruikt wordt zelfs niet veel ouder dan 100 jaar. De eerste keer dat er melding gemaakt wordt van het enneagram is in het begin van 20e eeuw. In dit tijdvak wordt het Enneagram in het Westen geïntroduceerd door de Armeen Georges Ivanovitch Gurdjieff. Volgens zeggen zocht Gurdjieff in het laatste kwart van de 19e eeuw spirituele en esoterische kennis, en vond hij die bij verschillende leermeesters, kloosters en stromingen in Azië en het Midden-Oosten. Hij maakte zijn inzichten vervolgens voor zichzelf tot een coherent geheel. En vanaf 1912 treedt hij daarmee nadrukkelijk in de openbaarheid in Rusland, met name in Sint-Petersburg en Moskou. Een groot deel van de essentie van zijn filosofieën en inzichten staat beschreven in het door een van zijn prominentste Russische leerlingen, de filosoof Peter D. Ouspensky(1878-1947) geschreven boek ‘Op zoek naar het wonderbaarlijke’ (met als ondertitel Fragmenten van een onbekende leer). Gurdjieff is een van de eersten, zo niet de eerste die, zo blijkt uit dit boek, melding maakt van het enneagram. Het enneagram vertegenwoordigt in zijn leer de relatie tussen de twee grootste levenswetten, door hem abstract beschreven als 'de wet van drie' en 'de wet van zeven'. Hoewel Gurdjieff beweerde dat je iets pas werkelijk begrijpt wanneer je het in een enneagram kunt plaatsen, ondernam hij geen poging de menselijke persoonlijkheid hiermee te beschrijven. Deze toepassing werd pas in de jaren '60 ontwikkeld door de in 1931 geboren Boliviaan Oscar Ichazo.

Onderstaande een citaat uit het boek ‘Op zoek naar het wonderbaarlijke’

“… het enneagram is een universeel symbool. Alle kennis kan in het enneagram worden uitgedrukt en met de hulp ervan worden geïnterpreteerd. En in dit verband weet de mens slechts juist zoveel als hij in het enneagram kan leggen, dat wil zeggen: die kennis die hij ook metterdaad begrijpt. Als hij het niet in het enneagram kan leggen begrijpt hij het ook niet. Voor de mens die bij machte is er gebruik van te maken, maakt het enneagram boeken en bibliotheken volkomen overbodig. Letterlijk alles kan in het enneagram worden gelegd en eruit worden gelezen. Iemand kan zich moederziel alleen in de woestijn bevinden, maar als hij het enneagram in het zand tekent kan hij er de universele wetten van de schepping uit aflezen. En iedere keer als hij dat doet kan hij er iets uit leren, iets dat hij eerder nog niet wist. Als twee mensen die verschillende scholen hebben bezocht elkaar ontmoeten, kunnen zij het enneagram tekenen en zullen zij met behulp daarvan in staat zijn uit te maken wie van hen de meeste kennis bezit en dientengevolge op een hoger plan staat. Zo weten zij wie de wijzere is, wie de leraar en wie de leerling... Het enneagram is een schematisch diagram van een eeuwigdurende beweging.”

De Franse filosoof R.A. Schwaller de Lubicz, vult bovenstaande citaat in zijn boek "Le Temple de l'Homme" aan met de volgende tekst:
Esoterisch gezien is de mathematische relatie waarin een getal zich tot de Eenheid verhoudt de sleutel tot de aard van dat getal, omdat alle getallen als delen van de Eenheid moeten worden beschouwd. Zowel het getal Drie als het getal Zeven zijn getallen van de "eeuwigdurende beweging". Als zij in eenheden worden verdeeld, laten zij zich tot het oneindige delen.
1 : 3 = 0,333333333333
1 : 7 = 0,142857142857

De ideeën van Gurdjieff met betrekking tot de "eeuwigdurende beweging" van de getallen drie en zeven is ook gebaseerd op bovenstaande tekst. Zowel Gurdjieff als de Lubicz maken hier de denkfout dat de repeterende eigenschappen van deze breuken absoluut zijn. De repeterende eigenschappen van breuken worden namelijk bepaald door het talstelsel waarin een deling wordt uitgevoerd. Als je b.v. de deling 1 : 7 uitvoert in het veertientallig stelsel komt er exact 0,2 als antwoord uit. Als je voor deze deling b.v. het negentallig stelsel gebruikt ontstaat de repeterende breuk 0,125125…, wat dus aangeeft dat de eeuwigdurende beweging relatief is. Daar het ontwerp van het enneagram volledig gebaseerd is op het tientallig positie stelsel kan het nooit ouder zijn dan de kennis van het delen in het tientallig positie stelsel. Het tientallig positie stelsel werd in Europa ingevoerd zo rond het jaar 1100. De Arabische cijfers en het tientallig stelsel waar wij mee werken zijn zo rond 200 v.Chr. door Hindoes ontwikkeld. Dit systeem is door de Arabieren verder ontwikkeld en pas rond het jaar 800 door hen goedgekeurd waarna het via Spanje in Europa terecht gekomen is. Voor 1600 werd voor het rekenen met niet-gehele getallen normaal gesproken gewerkt met algemene breuken, gebaseerd op handige noemers. Er waren wel gestandaardiseerde methoden die met 60-tallige breuken werkten, maar over het algemeen was het heel moeilijk om aan de breuk te zien in hoeverre die het gewenste niet-gehele getal werkelijk benaderde. Decimale breuken werden al wel gebruikt, maar alleen om te kunnen worteltrekken. In het dagelijks leven werkte men daar niet mee. In 1586 schreef Simon Stevin zijn beroemde werk De Thiende, waarin hij het algemeen gebruik van breuken op basis van het tientallig positie stelsel beschreef. Hij gebruikte daarvoor nog niet de notatie met een decimale punt of decimale komma zoals wij dat nu doen, maar een notatie waar achter elk cijfer in een cirkel de (negatieve) macht van 10 kwam te staan die op dat cijfer van toepassing was. Wat wij nu als 6,87 schrijven, schreef Simon Stevin als 6⓪8①7②. Pas toen Bartholomaeus Pitiscus in zijn trigonometrische tabellen in 1612 de decimale scheiding in de vorm van een punt gebruikte en dit gebruik in 1614 door John Napier in zijn artikelen over logaritmen werd erkend, werd de huidige notatie van de decimale breuk in gebruik genomen. De conclusie die je hier uit kunt trek is dat het enneagram pas na 1600 ontstaan kan zijn.

Het is ontzettend moeilijk om betrouwbaar materiaal te bemachtigen met betrekking tot de historie van het Enneagram. Na lang zoeken en de nodige aanbevelingen kwam ik tenslotte uit bij het boek “Het Enneagram en het team in jezelf” van Frank Schaper en Azwin Ressang. Beide heren hebben een respectabele staat van dienst en wekte bij mij voldoende vertrouwen. Het probleem is echter dat mensen die zich overgeven aan het typeren met het Enneagram, niet meer instaat zijn om op een nuchtere manier naar het symbool an sich te kijken. Het onderstaande citaat uit het boek geeft aan wat hun houding t.o.v. het symbool is:

“Onze conclusie luidt dat aan de lijnen in het bekende Enneagram-symbool geen speciale betekenis moet worden gehecht en dat het teken feitelijk niet meer is dan een mooi logo”

Ik ben zelf van mening dat de oorspronkelijke kracht van het symbool ligt in de mathematische structuur ervan. Beide heren staan er niet bij stil dat zaken als Enneatypes en basisemoties pas later aan het Enneagram zijn vastgeplakt en daarna een eigen leven zijn gaan leiden. Mogelijk hebben de persoonlijkheidsmodellen hun waarde, maar ze hebben feitelijk niets met het symbool an sich te maken. Voor mij is het symbool het Enneagram.

De grondlegger van het huidige Enneagram, Gurdjieff is volgens het boek niet de meest betrouwbare figuur. Hij staat bekend als een leugenaar en gebruikte buitensporige beweringen om zijn leerlingen tot spirituele verandering te shockeren. Gurdjieff zelf beweerde zijn kennis met betrekking tot het Enneagram opgedaan te hebben bij de soefi’s. Sommige soefi-ordes blijken ook gebruik te maken van een bepaalde vorm van het Enneagram. De spiritueel leider van de Noord-Amerikaanse tak van de soefi-orde Naqshibadi, Sheikh Hissam Kabbani claimt zelfs dat een van zijn voorgangers Gurdjieff in het soefi Enneagram heeft ingewijd. Ook het soefi Enneagram heeft een opbouw waaruit duidelijk naar voren komt dat het gebaseerd is op de deling 1 / 7 in het tientallig stelsel. Het soefi-Enneagram werd echter niet gebruikt voor persoonlijkheidsanalyse maar voor het stimuleren van het individuele menselijk bewustzijn. Het onderstaande voorbeeld laat het soefi-Enneagram zien.

Daar het soefi-Enneagram ook gebaseerd is op een breuk in het tientallig stelsel, mag je aannemen dat het pas na 1600 ontstaan is. Het symbool dat Gurdjieff gebruikte is nergens anders in het histories materiaal te vinden. Hij beweerde bovendien dat het Enneagram ‘iets exclusiefs van zijn leer was’. Het woord ‘enneagram’ bestond toen al wel, maar werd in een boek uit 1665 van de jezuïtische priester Kircher voor een andere vorm gebruikt, een geometrische figuur bestaande uit drie gelijkzijdige driehoeken, zoals hieronder te zien is. Volgens Ichazo kwam deze figuur ook al voor in de boeken van de Catalaanse filosoof Raimundus Lullus (1235-1316).

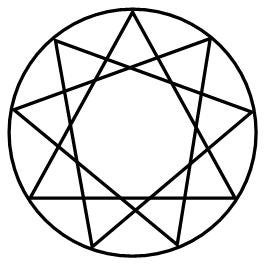
Het heeft er alle schijn van dat Gurdjieff ‘zijn’ Enneagram- symbool zelf bedacht heeft, daarbij geïnspireerd door het soefi-Enneagram en de tekening van Kircher.

Onderstaande het Enneagram zoals dat tegenwoordig gebruikt wordt.

Het huidige Enneagram geanalyseerd
 

Na deze lange inleiding wil ik nu eerst het Enneagram zoals dat gebruikt wordt in het alternatieve circuit aan een analyse onderwerpen. De figuur bestaat uit twee afzonderlijke delen, waarvan alleen het deel dat gevormd wordt door de deling 1 : 7 berekend kan worden, de driehoek die de figuur completeert is er gewoon bij verzonnen. Er bestaat geen enkele deling met gehele getallen die deze driehoek kan vormen. De figuur die door de deling 1 : 7 word gevormd wordt ook niet correct weergegeven. De figuur is getekend in een cirkel met 9 punten, terwijl het tientallig stelsel 10 getallen heeft, de nul telt namelijk ook mee. Onderstaande is de figuur te zien zoals het hoort. Het probleem is nu dat de resterende punten geen driehoek meer vormen. Ook de naamgeving klopt dan niet meer, omdat ennea namelijk negen betekent. De oorspronkelijke figuur is met voorbedachten rade geschonden om zo een driehoek toe te kunnen voegen en daarmee een mooiere coherente symmetrie te krijgen.

De bovenstaande versie van het Enneagram is evt. wel te complementeren met een figuur dat door deling is ontstaan. Voor deze aanvulling moet echter gebruik gemaakt worden van een deling die niet echt elegante oogt. Onderstaande figuur, die er op zich best aardig uitziet,  laat zien dat voor deze oplossing gebruik gemaakt wordt van de deling 4 / 101.

De eigenschappen symmetrie en herhaling van de deling 1 : 7 zijn niet uniek. Een groot gedeelte van de delingen met een repeterend karakter hebben deze eigenschappen gemeen. Een gedeelte van de delingen met een repeterend karakter geeft een figuur dat niet symmetrisch is. Als dit het geval is heeft de complementaire figuur een spiegelsymmetrie. De complementaire figuur ontstaat bij een deling met de zelfde noemer, en een teller die gelijk is aan de noemer min de oorspronkelijke teller. Als de oorspronkelijke deling 1 / 7 is, is de complementaire deling 6 / 7.

Onderstaande enkele voorbeelden van delingen die een symmetrisch figuur geven.

Onderstaande drie niet symmetrische figuren met hun complement

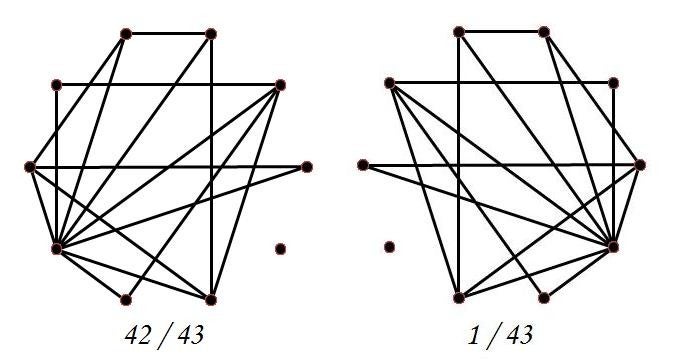
De deling 1 / 7 geeft in meerdere talstelsels het Enneagram. De enige afwijkende figuur ontstaat in het 5tallig stelsel, omdat daar het aantal punten op de omtrek maar 5 is. Dit zorgt er voor dat er twee punten samenvallen.
Onderstaande figuur laat zien welke talstelsels nog meer het Enneagram opleveren en hoe het Enneagram er in het 5tallig stelsel uitziet. De tussenliggende waarden leveren geen symmetrisch figuur op.

Het Enneagram constueren met behulp van een getallenreeks

Het deel dat gevormd wordt door de deling 1/7 kan ook geconstrueerd worden vanuit getallenreeksen. De reeksen die daar voor in aanmerking komen ontstaan door herhaald vermenigvuldigen van de voorgaande waarde in de reeks en het resultaat daarna met een modulo functie te bewerken. Onderstaande figuur met als vermenigvuldigingsfactor 5 laat zien hoe dit in zijn werk gaat. Als de modulo waarde een zevenvoud is, is er ook altijd een startwaarde en vermenigvuldigingsfactor te vinden die het Enneagram deel oplevert. Door de modulo waarde 7 is het aantal punten ook 7, en is de naam Enneagram niet correct meer.

DNA met het Enneagram

De correcte getallencirkel (inclusief de 0) die gebruikt wordt om het Enneagram en vergelijkbare figuren te tekenen heeft een eigenschap die het mogelijk maakt om de getallenreeksen die deze figuren vormen weer te geven als DNA reeksen. Onderstaande getallencirkel van het tientallig stelsel laat zien dat de getallen die naast elkaar staan bij elkaar opgeteld altijd de waarde 9 geven. Het linker getal heeft een relatie met het rechter getal.

Indien je de waarden op de cirkel met modulo 4 bewerkt wordt iedere getal teruggebracht naar een waarde kleiner dan 4, en ontstaat de situatie zoals hieronder is weergegeven. De relatie van het linker getal met het rechter getal blijft. Iedere 0 is gekoppeld aan een 1 en ieder 2 is gekoppeld aan een 3. Indien je nu de getallen omcodeert volgens de tabel die naast de figuur staat, ontstaat er een DNA gelijkende structuur.

Indien je in de bovenstaande situatie de DNA-letters op de cirkel weergeeft, en je tekent het Enneagram dan krijg je onderstaande figuur. Indien je het Enneagram volgt vanaf punt 1 richting de 4 krijg je de reeks zoals die ontstaat met de deling 1 / 7.  Indien je het Enneagram volgt vanaf punt 8 richting de 5 krijg je de reeks zoals die ontstaat met de deling 6 / 7. Indien je de letters langs het Enneagram noteert en naast elkaar zet, ontstaat een DNA gelijkende reeks waarvan de volgorde bepaald is door het Enneagram.

Indien je deze techniek toepast op andere delingen die een symmetrisch patroon vormen wordt het aantal DNA variaties oneindig groot. Indien je voor de noemer van de deling een groot priemgetal neemt is de kans groot dat er een lange DNA-reeks ontstaat. Onderstaande een voorbeeld met de deling 1 /17 en 16 /17 waarbij een DNA-reeks van 16 letters ontstaat.