Het Magisch vierkant

Een magisch vierkant is een vierkant van n bij n hokjes waarin de getallen van 1 tot en met n² zijn ingevuld, op zo’n manier dat minstens elke kolom, elke rij en de beide diagonalen opgeteld dezelfde uitkomst geven. n moet altijd groter zijn dan 2. 

Magische vierkanten waren al bekend bij de Chinese wiskundigen voor het jaar 650 v. Chr en bij de Arabische wiskundigen al in de 7e eeuw, toen de Arabieren de noordwestelijke delen van het Indische subcontinent veroverde en daarbij de Indiase wiskunde en astrologie leerden gebruiken. De eerste magische vierkanten van orde 5 en 6 verschijnen in de Encyclopedie van de Broeders van Zuiverheid (Rasa'il Ihkwan al-Safa) een encyclopedie uit Bagdad zo rond het jaar 983. 

Het Lo Shu vierkant (3 × 3 magisch vierkant)

De Chinese literatuur van voor 650 v. Chr vertelt de legende van Lo Shu over de overstroming van de rivier de Lo. In het oude China was er een enorme overstroming. De grote koning Yu had geprobeerd om een kanaal te graven naar de zee om zo het water af te voeren. Tijdens het graven werden er offers gebracht in de hoop de rivier gunstig te kunnen stemmen. Het offer ritueel werd echter steeds onderbroken door een schilpad die uit de rivier kwam gekropen. Na dat dit een aantal keren gebeurd was ontdekte iemand dat deze schilpad een merkwaardige patroon op zijn schild had. Het was een figuur van ronde stippen die in een rasterpatroon geplaatst waren van drie bij drie, zodanig dat de som van deze stippen in elke rij, kolom en diagonaal 15 was.
15 is het aantal dagen in elk van de 24 cycli van het Chinese zonnejaar. De Chinezen beschouwde dit als een teken dat er 15 offers gebracht moesten worden, 1 voor iedere dag in de cyclus, na de uitvoering van deze offeranden stopte de overstroming.

Volgens de meer officiële kanalen is de Loh-Shu bedacht  door de wiskundig geschoolde keizer Fuh-Hi. Keizer Fuh-Hi wordt gezien als de grondlegger van de Chinese beschaving. Het Loh-Shu vierkant belichaamt het oosterse concept van Yin en Yang. De oneven getallen worden gepresenteerd met witte punten welke het Yang voorstellen, de even getallen door zwarte punten die het Yin voorstellen. Voor de Chinezen zijn de oneven getallen (Yang) het symbool van de hemel en de even getallen (Yin) het symbool voor de aarde.

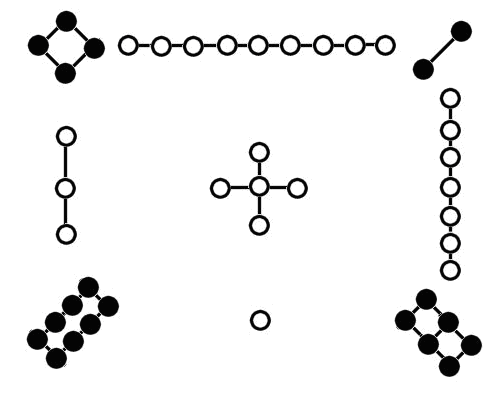
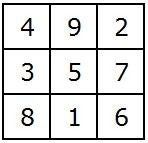
Het Lo Shu vierkant , zoals het magische vierkant in China genoemd wordt, is het unieke normale magische vierkant van orde drie, waarbij 1 aan de onderkant en 2 aan de rechterbovenhoek is gepaaltst. Elk magische vierkant van orde drie kan verkregen worden uit het Lo Shu vierkant door rotatie of spiegeling. Het Lo Shu vierkant wordt in astrologische kringen ook wel het Saturnes vierkant genoemd. Onderstaande een Saturnes talisman met bijbehorende symbolen.

Het symbool linksboven in de talsiman is het Saturnus symbool uit de astrologie, het symbool middenboven is het Saturnus sigil (magisch zegel). Het Saturnus sigil kan als volgt uit het magisch vierkant gegenereerd worden:
Verdeel de nummers in het vierkant in 3 groepen van 3, (1 2 3) (4 5 6) (7 8 9).  Trek lijnen tussen deze nummers zodat onderstaande figuur ontstaat.

Het bovenstaande vierkant staat ook bekend als het Vrijmetselaars vierkant. Door in dit vierkant het Vrijmetselaars zegel te plaatsen krijg je onderstaande figuur. De punten van de passer en driehoek vormen numerieke codes die door de vrijmetselaars gebruikt worden om o.a. hun loges een speciale betekenis te geven.

Magische vierkanten fascineren de mensheid al eeuwen, er zijn vondsten bekend die meer dan 4000 jaar oud zijn. Ze zijn te vinden in veel culturen, waaronder Egypte en India , gegraveerd op steen of metaal en gedragen als talisman. Het geloof is dat magische vierkanten beschikken over astrologische en profetische kwaliteiten. Het gebruik ervan waarborgt een lange levensduur en beschermt tegen ziekten. 

De Kubera-kolam is een vloerschildering in de vorm van een magisch vierkant dat gebruikt wordt in India. Het is een magisch vierkant van orde drie dat wat nummering betreft afwijkt van de norm. Het is in wezen hetzelfde vierkant als het Lo Shu Vierkant waarbij alle waarden met 19 verhoogd zijn, waardoor een magische constante van 72 ontstaat.

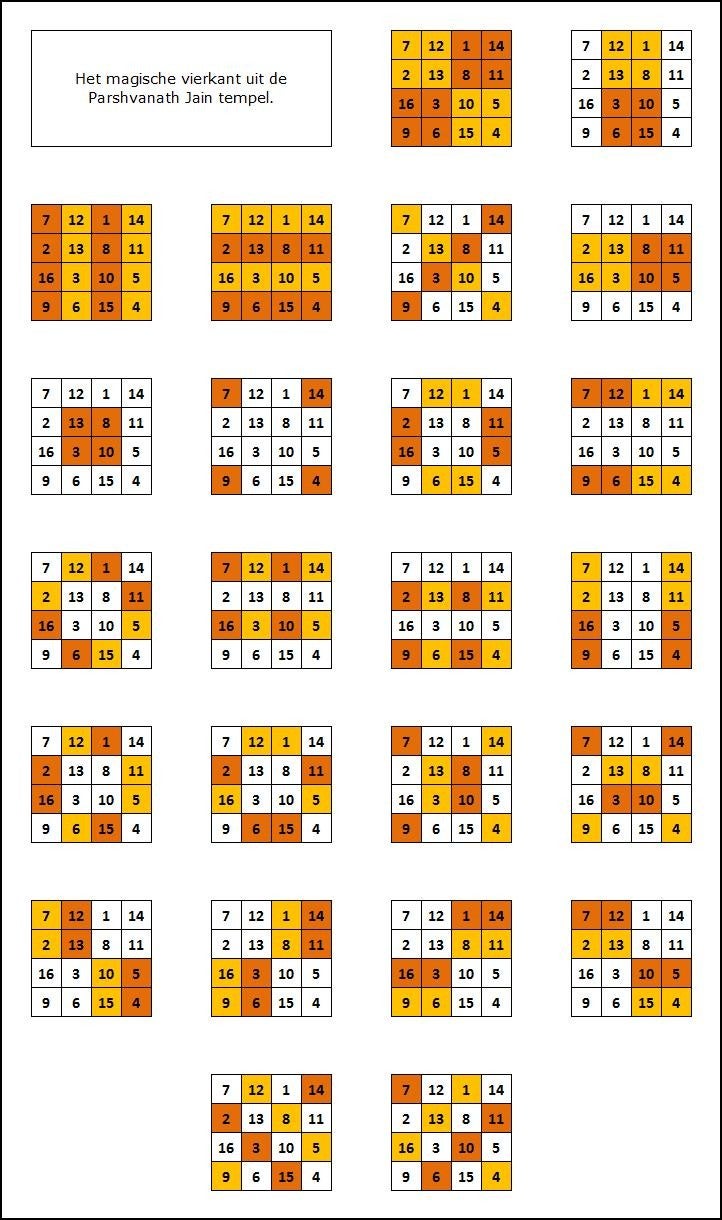
Ook in India werd en wordt het 3x3 magische vierkant gebruikt bij Vedische rituelen en wordt daar de Ganesh yantra genoemd. Een bekend 4x4 magische vierkant dat in India gebruikt wordt is te zien in Khajuraho in de Parshvanath Jain tempel. Het dateert uit de 10e eeuw.

Dit vierkant wordt de Chautisa Yantra genoemd, omdat elke rij, kolom, diagonaal, alle 2x2 sub-vierkanten, de hoeken van elk 3x3 en 4x4 vierkant, de twee sets van vier symmetrische nummers (1 +11 +16 +6 ), (12 +2 +15 +5), en de som van de middelste twee ingangen van de twee buitenste rijen en kolommen (12 +1 +6 +15 ) en (16 +11 +2 +5) de som 34 opleveren.

Een ander bijzonder vierkant is het vierkant op de gravure Melencolia I van Albrecht Dürer. De Chautisa Yantra is echter veel uitgebreider dan Melencolia I. Albrecht Dürer heeft in zijn vierkant het jaartal van zijn creatie 1514 verwerkt, en heeft daarvoor concessies moeten doen t.o.v. de Chautisa Yantra. Het aantal unieke mogelijkheden om een som van 34 te krijgen met de getallen 1 t/m 16 is 86. Het vierkant van Albrecht Dürer kent 38 mogelijkheden om een symmetrisch patroon te creëren, de Chautisa Yantra 52. In onderstaande figuren zijn de mogelijkheden van beide vierkanten weergeven.

Het vierkant van Albrecht Dürer is volgens eenvoudige basis principes geconstrueerd. In onderstaande animatie is te zien hoe de figuur systematisch opgebouwd kan worden. 

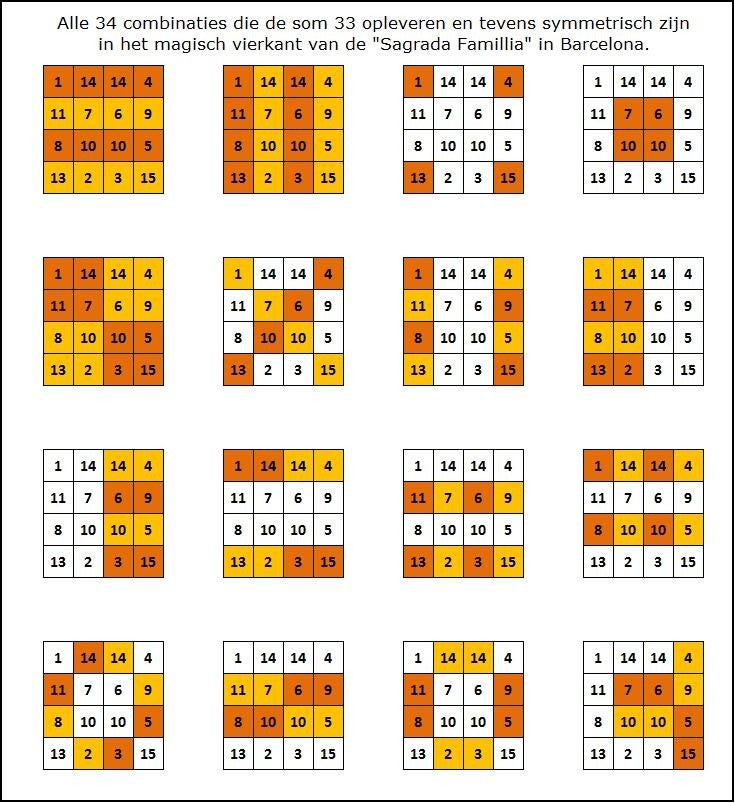
Op onderstaande foto is een deel te zien van de "La Sagrada Familia" in Barcelona. Op de muur van deze kerk is een bijzonder magisch vierkant te vinden. De som van de getallen van dit vierkant is steeds 33. Dit effect kan alleen gerealiseerd worden door af te wijken van de standaard methode. Het vierkant mist de getallen 12 en 16, en heeft de getallen 10 en 14 dubbel. Het getal 33 is een heilig getal voor de vrijmetselaars. De ontwerper Antoni Gaudí is tussen zijn twintigste en dertigste levensjaar een tijdlang lid geweest van de vrijmetselarij. Dit gegeven insinueert dat de ontwerper iets van zijn ideeën verwerkt heeft in deze kerk. Volgens de officiële documentatie verwijst het getal 33 naar de leeftijd waarop Jezus Christus stierf. Het is echter zeer verdacht dat het magisch vierkant opgezet is volgens een concept dat veel gebruikt wordt door de vrijmetselaars.

Het bijzondere aan dit vierkant is dat de getallen volgens een bepaald patroon gerangschikt zijn zoals in onderstaande afbeelding te zien is. Deze rangschikking zie je ook terug bij het magische vierkant van Albrecht Dürer, alleen is de richting waarin de getallen lopen precies omgekeerd. In deze rangschikking zie je een dubbele passer en winkelhaak formatie zoals die bij de vrijmetselaars gebruikt wordt. Ook Albrecht Dürer had banden met de vrijmetselarij en is zeer waarschijnlijk lid geweest van de Neurenberg Loge.

Het magisch vierkant van de Sagrada Famillia is eenvoudig te construeren vanuit het magisch vierkant van Albrecht Dürer. Indien je het vierkant van Dürer 180 graden draait en daarna de getallen 11, 12, 15 en 16 met 1 verminderd, is het vierkant compleet.

Een ander type magisch vierkant zijn de Franklin magische vierkanten. Deze vierkanten voldoen niet helemaal aan de eisen van een zuiver magisch vierkant, omdat de diagonalen niet voldoen aan de magische som. Deze vierkanten hebben echter wel een aantal andere zeer bijzondere eigenschappen die hieronder genoemd worden:
1. De som van de rijen en kolommen zijn telkens gelijk aan de magische som,
2. De som van de halve rijen en kolommen zijn telkens gelijk aan de helft van de magische som,
3. Gebogen diagonalen, die halverwege van richting veranderen, zoals 52-3-5-54-10-57-63-16
   en 52-3-5-54-43-28-30-45, zijn telkens gelijk aan de magische som, ook als je ze verschuift,
4. Elk vierkantje van 2 bij 2 heeft een vaste som, gelijk aan 4 maal de magische som gedeeld door
   het aantal kolommen.

Welke methode Franklin gebruikt heeft om zijn vierkanten te ontwerpen is niet bekend. Deze vierkanten zijn met wat moeite te creëren volgens de methode die ik boven heb beschreven bij het vierkant van Albrecht Dürer. In onderstaande plaatjes laat ik zien hoe je dit doet. Plaats de getallen van 1 t/m 64 in het vierkant zoals in het linker figuur te zien is. Draai de geel gekleurde rijen om, zodat het rechter figuur ontstaat. De som van de rijen en kolommen is nu al gelijk aan de magische som 260.

Verplaats in onderstaande afbeelding de gele kolom in de linker figuur naar links en daarna de bovenste 2 rijen naar onder. Het vierkant dat nu ontstaan is heeft ook de som van de halve kolommen en rijen gelijk aan de halve magische som.

Verwissel tenslotte de bovenste en onderste twee rijen onderling en de figuur is klaar.

Deze methode werkt natuurlijk ook voor grotere vierkanten. Onderstaande de afbeeldingen die horen bij de methode voor het 16x16 vierkant, zonder verdere omschrijving.

Een Franklin magisch vierkant van 12x12 is niet mogelijk. Ik ben er wel in geslaagd met bovenstaande methode een 12x12 vierkant te maken dat voldoet aan alle voorwaarden behalve de gebogen diagonalen. De gebogen diagonalen zijn horizontaal om en om 868 en 872 en vertikaal om en om 726 en 1014.

Volgens Johan Oldenkamp in zijn boek "Cosmische code" is het 3x3 Lo Shu vierkant het kleinste vierkant van een serie van 7 Chinese vierkanten. In onderstaande figuur is deze serie van 7 vierkanten weergegeven. Het vreemde is echter dat het tweede vierkant het omgekeerde Albrecht Dürer vierkant is. De vraag is, heeft Dürer het vierkant geleend van de Chinezen of verkoopt Oldenkamp onzin. Alle even vierkanten hebben de 1 linksboven en het grootste getal rechtsonder. Alle oneven vierkanten hebben de 1 middenboven en het grootste getal middenonder.  

Onderstaande figuur is een door mij zelf gecreëerd vierkant van de orde 16. Het centrum van het vierkant kan ieder echt magische vierkant van orde 4 zijn. In het onderstaande voorbeeld zie je wisselend het vierkant van Albrecht Dürer en de Chautisa Yantra. De som van de horizontale, verticale en diagonale lijnen is steeds 2056.

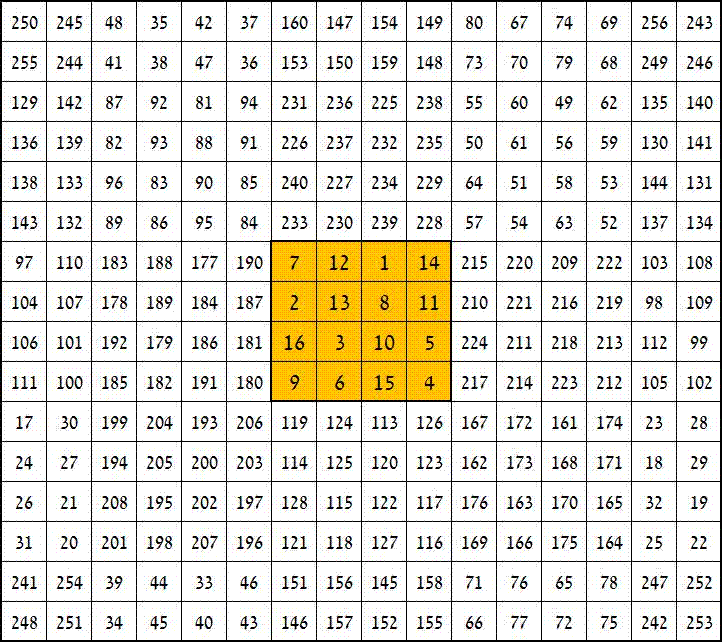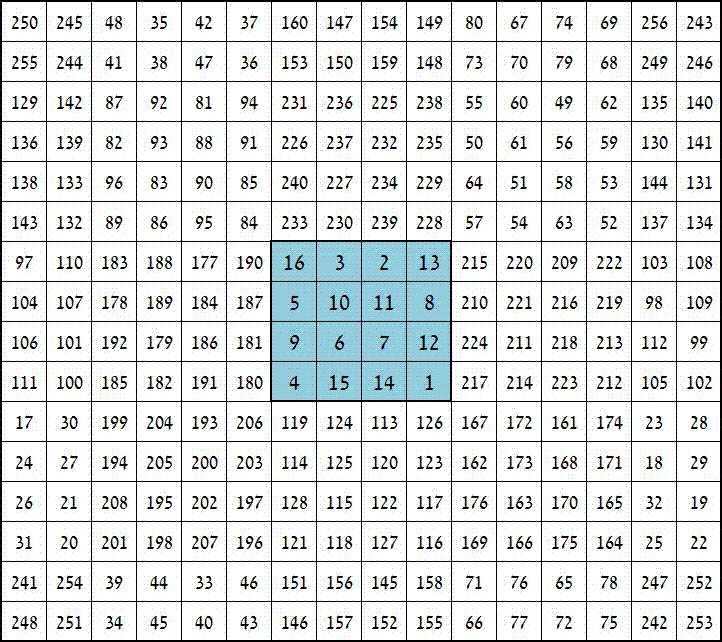
Doordat het vierkant in combinatie met de Chautisa Yantra een panmagisch vierkant is kun je de figuur scrollen zonder dat het zijn magische eigenschappen verliest. Het effect dat dan ontstaat is te zien in onderstaande animatie.

Onderstaande Hebreeuwse vierkant is het Chai square, ook wel het vierkant van het leven genoemd. Het Chai square is een panmagisch vierkant van de orde 4 waarin de getallen 1 t/m 8 ieder 2x voorkomen. De magische som van de getallen is steeds 18. Dit vierkant dankt zijn naam aan het feit dat het Hebreeuwse woord voor leven in gematria de waarde 18 heeft. Het aantal mogelijkheden om de waarde 18 te vormen is net zo groot als bij de Chautisa Yantra.

Onderstaande een panmagische vierkant met een magische som van 10. Alle getallen van 1 t/m 4 komen 4 maal voor. Ook alle 2x2 vierkanten hebben de magische som van 10.

Onderstaande een strak geordend superpanmachisch vierkant van 10x10 waarin alle getallen van 1 t/m 25 vier maal voorkomen. Alle horizontale, vertikale, diagonale, pandiagonale en gebroken diagonale lijnen hebben de magische som van 130.